Enhanced sampling using autoencoders

Understanding of physical systems depends crucially on sufficient sampling of system conformations. However, the presence of energy barrier generally impedes efficient sampling. One way to solve this issue is to add biasing forces to “pull” the system along important directions (which are encoded in “collective variables”). Finding such directions is essentially a dimensionality reduction problem, where we want to reduce high-dimensional conformational representations (e.g. encoded as Cartesian coordinates of atoms) to low-dimensional embeddings. For sampling problem, we have some additional requirements for dimensionality reduction:

1. we need to have an explicit function mapping from high-dimensional space to low-dimensional space

2. time and space complexity should be O(N) to be efficient

3. low-dimensional embeddings should be invariant under arbitrary translations and rotations of molecules, as we are not interested in rigid movement of molecules

To satisfy 1 and 2, we use autoencoders. To satisfy 3, we borrow idea of data augmentation from image recognition. The idea is, when an image of cat is shifted/rotated/scaled, it should still be classified as a cat, not anything else. Therefore, the same molecular conformation with different center-of-mass positions or orientations should still be mapped to the same outputs.

How do we encode this idea in an autoencoder? We require that all input conformations are mapped to the same “aligned” conformation. To illustrate the idea, we use cat images as input and show how they are projected onto low-dimensional space.

Firstly let’s see what happens if we use traditional autoencoders. Recall that traditional autoencoders faithfully reconstruct whatever we put in as inputs. Therefore in this case, the same “cat conformation” (sitting quietly, smiling with its tail pointing upwards) with different orientations will be mapped to different outputs. Hence in order to be mapped to different outputs,low-dimensional embeddings must be different.

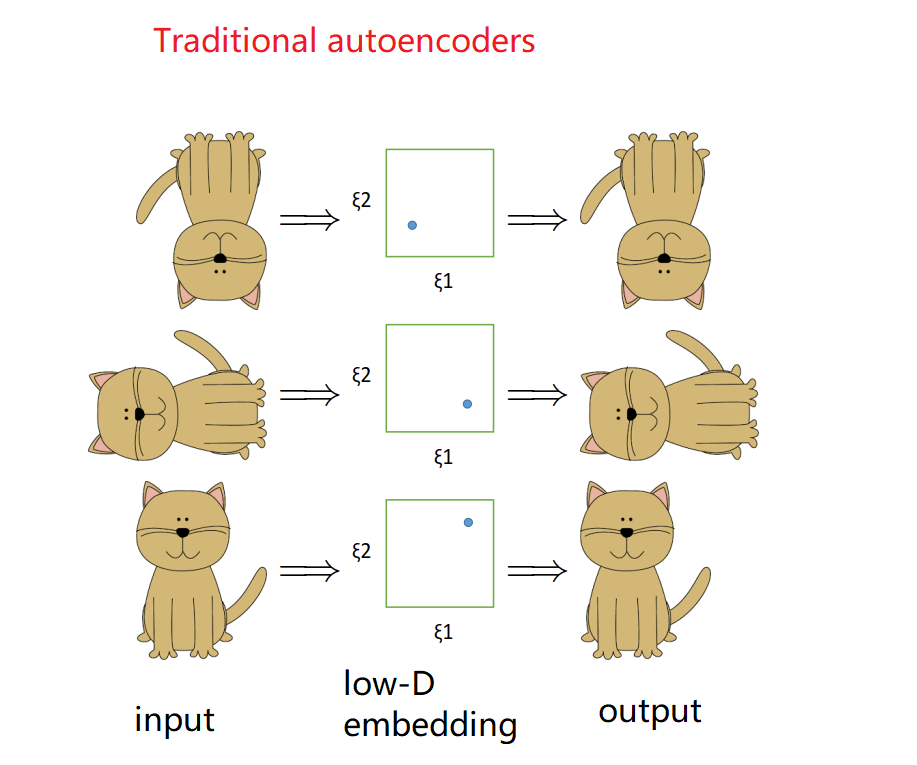
Now consider autoencoders with data augmentation. We require all these cats be mapped to the same “aligned” outputs:

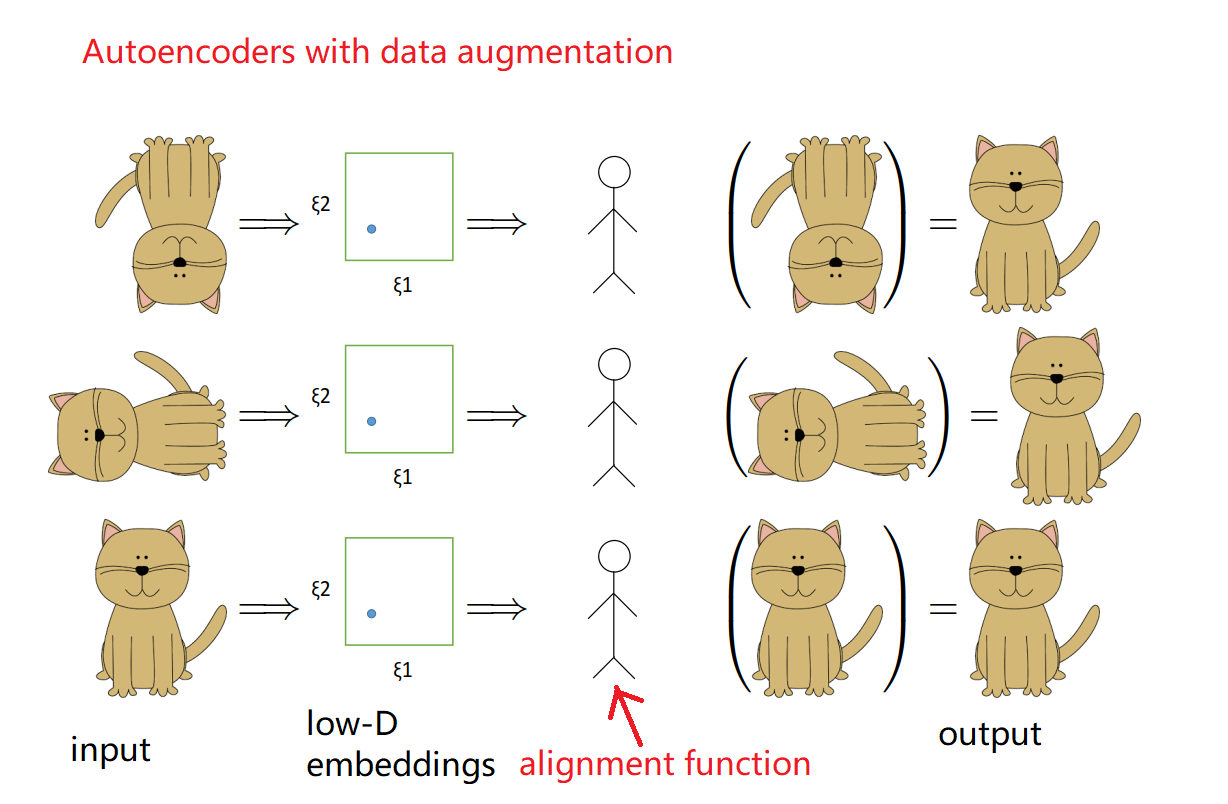
Here we use an alignment function (“little human”) to generate expected outputs for inputs, such that same “cat conformation” with different orientations are mapped to the same output. Therefore low-dimensional embeddings must be the same as well.

To implement this, we simply need to use following error function for neural network training:

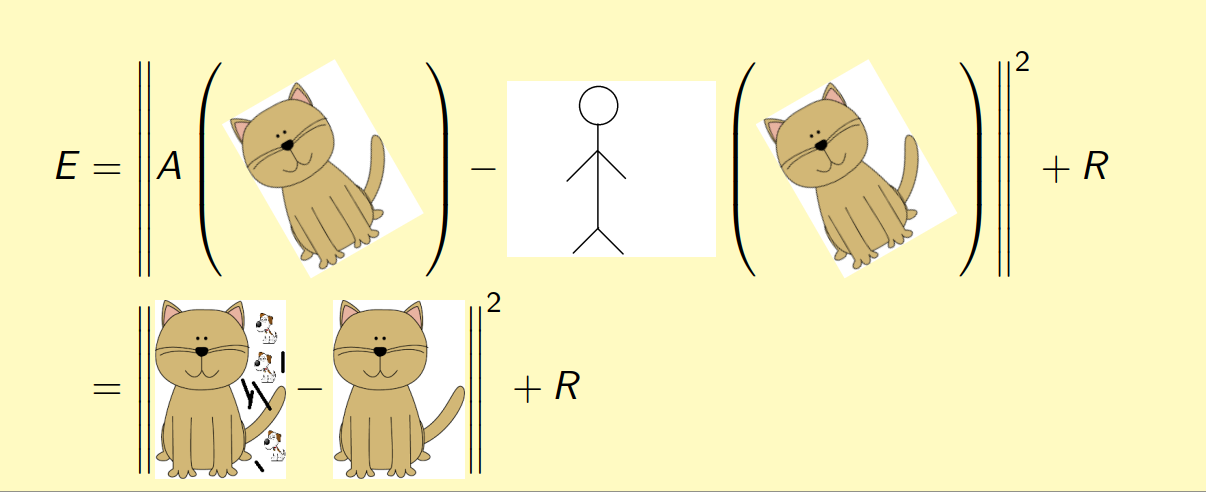
where A(.) is autoencoder output, “little human” is the alignment function, “cat” is the input conformation, R is the regularization term. What are those sticks and snoopy dogs in the autoencoder output? They represent reconstruction error, as the autoencoder cannot perfectly reconstruct every detail and there is information loss when doing dimensionality reduction.

We use this idea together with enhanced sampling techniques to improve sampling efficiency, and have built an open-source package available here.

For more information, checkout this paper.