Hierarchical autoencoders
In a typical dense layer in a neural network, all nodes are equivalent, meaning that if we swap weights of any two nodes, the output will stay unchanged. Therefore, unlike PCA, an autoencoder cannot sort “principal components” (which we call “collective variables” or CVs for autoencoders) by their importance.
To make sure autoencoder CVs are sorted by important, we need to break the equivalence and rewire the neural network. Based on idea of NLPCA, we design two following autoencoder architectures:
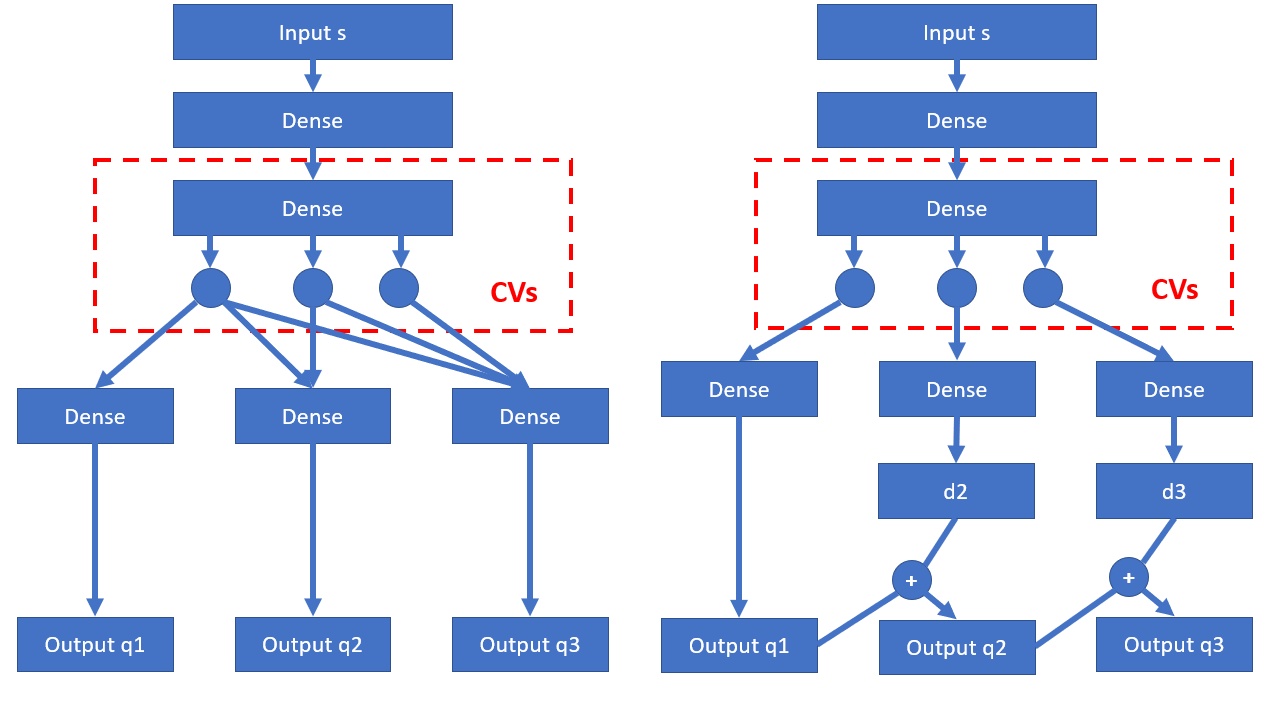
On the left hand side, we have a “collective hierarchical autoencoder”. The idea is for an input s, instead of just creating one reconstructed output, we create n outputs (n is dimensionality of low-dimensional space, n = 3 in the diagram above). Now here is the key: we break the equivalence of nodes in the CV layer (which encodes CVs), such that the information of first output (q1) only comes from CV1, and information of second output (q2) only comes from CV1, CV2, and so on. The loss function L is the average reconstruction loss of these reconstructed outputs L = ((s - q1)^2 + (s - q2)^2 + (s - q3)^2) / 3. Since CV1 participates in all reconstructions, it should contain most important information. CV2 participates in all reconstructions except output q1, therefore it should be second important. By doing this, we get the low-dimensional CVs ranked by their importance.
On the right hand side, it is a different variant we call “boosted hierarchical autoencoder”. The idea is based on boosting, which is also the idea behind boosted trees and residual neural networks. As the same with previous variant, first output q1 is constructed from CV1 only. What is different is about following nodes: for CV2, instead of directly collaborating with CV1 to construct q2, it aims to fit the residual error that has not been learned by the CV1. Let the fitted result be d2 (as indicated in the diagram), then the second constructed result q2 is q2 = q1 + d2. This is similar to a boosted regression tree which adds several tree outputs to get the final output. Similarly, CV3 fits residual error that has not been learned by CV1 and CV2 as d3, and corresponding constructed output is q3 = q1 + d2 + d3. Again, loss function is still the average reconstruction loss L = ((s - q1)^2 + (s - q2)^2 + (s - q3)^2) / 3. Following similar discussion, we can convince ourselves that CV1, CV2, CV3 are low-dimensional CVs sorted by importance.
Information about hierarchical autoencoders and their application in molecular simulations can be found here.